Questão de PET - Observe, abaixo, o gráfico de uma função definida por várias sentenças

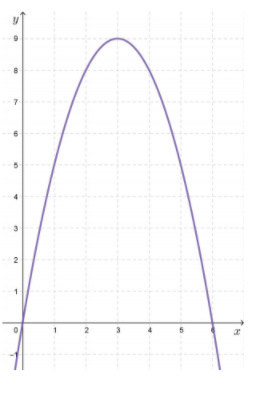
3.Observe, abaixo, o gráfico de uma função definida por várias sentenças envolvendo as leis de formação de funções polinomiais de 1o grau, de 2o grau e função constante.

Responda as questões a seguir.

a) Quais são os zeros ou raízes da função polinomial de 2° grau cuja lei de formação está envolvida na

definição da função f ? ____________________

b) Quais são as coordenadas do vértice da parábola, gráfico da função polinomial de 2° grau, cuja lei de

formação está envolvida na definição da função f ?_______________

c) Para -2≤ x ≤ 0, a lei de formação envolvida na definição da função f é de uma função polinomial de 1° grau, de 2° grau ou função constante? ____________________ Nesse intervalo, a função é crescente ou decrescente? ______________________

d) Para 1 ≤ x ≤ 3, a lei de formação envolvida na definição da função é de uma função polinomial de 1° grau, de 2° grau ou função constante? ____________________ Nesse intervalo, a função f é crescente

ou decrescente? ______________________

e) Para quais valores de x , a função f é constante? _________________ Para esses valores de x, qual é o valor de f(x)? _________________

RESPOSTA:

Questão de PET - A parte interior de uma taça foi gerada pela rotação de uma parábola

2. A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura ao lado. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. A função real que expressa a parábola, no plano cartesiano da figura, é f(x) = ---- 3/2x² - 6x + C , onde c é a medida da altura do líquido contido na taça, em centímetros. Qual a altura do líquido ou o valor de

C da função?

RESPOSTA:

Questão de PET - Dada a função quadrática definida por f(x) = x² - 4x + 4

1. Dada a função quadrática definida por f(x) = x² - 4x + 4, responda as questões a seguir.

a) Quais são os coeficientes a, b e c da lei de formação dessa função? ___________________

b) Quais são as coordenadas do ponto de interseção entre o gráfico dessa função e o eixo x?

_______________

c) Qual é o valor do discriminante ∆ ?

d) Como ∆ é __________ que 0, quantos e quais são os zeros ou raízes dessa função? _____________

e) Quais são as coordenadas dos pontos de interseção entre o gráfico dessa função e o eixo x? _______

___________________________

f) Quais são as coordenadas do vértice da parábola, gráfico dessa função? _________________

g) Como a é __________ que 0, a concavidade da parábola, gráfico dessa função, é aberta para cima

ou para baixo? ___________ Nesse caso, o vértice da parábola é o ponto de mínimo ou de máximo da

função? ___________________.

h) Abaixo, preencha a tabela, determinando pontos do gráfico dessa função e, depois, construa o seu

gráfico no plano cartesiano.

RESPOSTA:

Questão de PET - Um golfinho realiza um salto cuja trajetória é uma parábola

4. Um golfinho realiza um salto cuja trajetória é uma parábola como a que está representada no gráfico ao lado. Responda as questões que seguem.

a) Qual foi a altura h, em metros, atingida pelo golfinho no ponto máximo do seu salto? __________ m

b) Qual foi o tempo, em segundos, que o golfinho

gastou para atingir a altura máxima? ___________ s

RESPOSTA:

Questão de PET - Observe, ao lado, o gráfico de uma função quadrática e responda as questões a seguir.

3. Observe, ao lado, o gráfico de uma função quadrática

e responda as questões a seguir.

a) Quais são os zeros ou raízes dessa função?
______________
b) Quais são as coordenadas dos pontos de interseção
entre o gráfico dessa função e o eixo x?
______________________
c) Quais são as coordenadas do vértice da parábola,
gráfico dessa função? ___________________
d) Quais são as coordenadas do ponto de interseção entre o gráfico dessa função e o eixo y? _______________
e) Como a concavidade da parábola é aberta para
___________, então o coeficiente a é maior ou menor que 0? ___________ Nesse caso, o vértice da
parábola é ponto de mínimo ou máximo da função?
______________
f) Quais são os coeficientes a, b e c dessa função?
___________________
g) Qual é a lei de formação dessa função?
_____________________

RESPOSTA: