- Explique qual é a relação entre as rochas, os minerais e os minérios.
RESPOSTAS DE LIVROS
PESQUISAR ESTE BLOG
quinta-feira, 31 de dezembro de 2020
Questão - Explique qual é a relação entre as rochas, os minerais e os minérios.
quarta-feira, 30 de dezembro de 2020
Questão de PET - Uma pessoa observa o ponto mais alto de um mastro (ponto A)
04. Uma pessoa observa o ponto mais alto de um mastro (ponto A) sob um ângulo de 30°. Considerando que a distância entre a pessoa e o mastro da bandeira no chão (segmento ) é de 25 metros e que a distância dos olhos dela ao chão (segmento ) é de 1,8 metros, calcule a medida aproximada da altura do mastro.
RESPOSTA:
Questão de PET - A figura abaixo que está representada fora de escala, mostra um barco partindo do ponto B
03. A figura abaixo que está representada fora de escala, mostra um barco partindo do ponto B em direção ao ponto C, levado por uma forte correnteza, segundo um ângulo de 60°. Se a largura do rio é 120 metros, qual a distância percorrida pelo barco até o ponto C?
RESPOSTA:
Questão de PET - Para relembrar as razões trigonométricas de seno (sen), cosseno (cos) e tangente (tg)
02. Para relembrar as razões trigonométricas de seno (sen), cosseno (cos) e tangente (tg) no triângulo retângulo que estão destacadas abaixo, calcule o valor da medida em cada uma das figuras a seguir, considerando a representação esquemática fora de escala.
a) X = ________ cm
b) X = ________ cm
c) X = ________ cm
d) X = ________ cm
e) X = ________ cm
f) X = ________ cm
RESPOSTA:
Questão de PET - Seguindo os dados acima, calcule a tangente de 60°
01. Seguindo os dados acima, calcule a tangente de 60° e depois preencha a tabela a seguir.
RESPOSTA:
Questão de PET - No PET VI, vimos o Teorema de Pitágoras.
02. No PET VI, vimos o Teorema de Pitágoras. Observe a figura abaixo e responda as questões a seguir.
a) Qual é a medida da hipotenusa (a)? a = ________cm
b) Qual é a medida do cateto adjacente ao ângulo ?
________cm
c) Qual é a medida do cateto oposto ao ângulo ?
________cm
d) Qual é a medida do cateto adjacente ao ângulo B?
________cm
e) Qual é a medida do cateto oposto ao ângulo B?
________cm
f) Determine:
g) Qual é a medida do perímetro desse triângulo? _________cm
h) Qual é a medida da área desse triângulo? ________cm2
i) Represente, na figura, a altura (h) desse triângulo em relação à hipotenusa. Qual é a medida dessa
altura? h = ________cm
j) No PET Volume VI, demonstrou-se as relações métricas no triângulo retângulo:
Vamos relembrar? Observe a figura abaixo. Use a medida da altura (h) que você calculou anteriormente
na letra i e aplique o Teorema de Pitágoras para encontrar as medidas (m e n) das projeções dos catetos
sobre a hipotenusa(a). m = ________cm e n = ________cm
Compare se a medida da altura (h) corresponde a mesma medida da altura que você calculou na letra i,
multiplicando m por n e efetuando a raiz quadrada sobre o produto encontrado:
Depois, confira se a soma das projeções corresponde a mesma medida da hipotenusa que você calculou na letra a usando o Teorema de Pitágoras:
Também compare as medidas de cada um dos catetos ao quadrado com o produto da hipotenusa pela
suas projeções correspondentes.
RESPOSTA:
Questão de PET - Agora é com você estudante! Escreva as razões trigonométricas
01. Agora é com você estudante! Escreva as razões trigonométricas do ângulo β da figura acima.
RESPOSTA:
terça-feira, 29 de dezembro de 2020
Questão de PET - Observe o triângulo retângulo desenhado abaixo
7 – Observe o triângulo retângulo desenhado abaixo. Faça uma rotação de 45° em torno do ponto B, no sentido anti-horário. Utilize régua e transferidor ou, então, trace um plano cartesiano sobre a figura, identificando o ponto B com a origem (0, 0), o que facilita executar o giro 45° sem o uso de um transferidor.
RESPOSTA:
Questão de PET - Observe o triângulo desenhado no primeiro quadrante do plano cartesiano
6 – Observe o triângulo desenhado no primeiro quadrante do plano cartesiano abaixo. Faça uma reflexão dessa figura em relação ao eixo das ordenadas e uma translação dessa figura para o quarto quadrante, deslocando 10 unidades.
RESPOSTA:
Questão de PET - Abaixo, temos um pentágono e um eixo de reflexão.
5 – Abaixo, temos um pentágono e um eixo de reflexão. Utilizando uma régua, faça a reflexão do pentágono.
RESPOSTA:
Questão de PET - Você conhece um cocar indígena
4 – Você conhece um cocar indígena? Abaixo, temos a figura de metade de um cocar desenhado no plano cartesiano. Faça a reflexão dessa figura para completar o desenho, colorindo a imagem refletida adequadamente.
Agora, responda.
a) Quais são as coordenadas dos nove vértices da figura que está desenhada a metade, os quais se encontram plotados no plano cartesiano?
b) Quais são as coordenadas dos sete vértices que teremos que determinar para completar a figura mencionada acima?
c) O que devemos fazer em relação às coordenadas dos sete vértices plotados no plano e não pertencentes ao eixo y para obter os sete vértices restantes para completar a figura mencionada acima?
A) Manter a abscissa e manter a ordenada.
B) Manter a abscissa e multiplicar a ordenada por – 1.
C) Multiplicar a abscissa por – 1 e manter a ordenada.
D) Multiplicar a abscissa por – 1 e multiplicar a ordenada por – 1.
d) O que fizemos, para completar a figura, foi determinar o simétrico, em relação ao eixo y, dos sete vértices plotados no plano e não pertencentes a esse eixo. Por que não precisamos determinar o simétrico, em relação ao eixo y, dos outros dois vértices plotados no plano e que pertencem a esse eixo?
e) Qual é a diferença entre translação e reflexão?
f) Quando estamos de frente para o espelho e levantamos o braço esquerdo, nosso reflexo levanta qual braço? Por que isso acontece?
RESPOSTA:
Questão de PET - Conhecemos três tipos de simetria: translação, rotação e reflexão
3 – Conhecemos três tipos de simetria: translação, rotação e reflexão. Relacione as imagens ao nome da simetria correspondente.
RESPOSTA:
Questão de PET - Agora responda as questões a seguir
2 – Agora responda as questões a seguir.
a) Quais são as coordenadas dos pontos que formam as extremidades da imagem original desenhada no plano cartesiano do tópico anterior? E do ponto central dessa imagem?
b) O que é uma translação? O que acontece com uma imagem quando a mesma é transladada? O que muda? O que se mantém?
c) Para fazermos a translação de uma imagem, como devemos proceder? O que deve ser feito em
relação às coordenadas dos pontos da imagem?
RESPOSTA:
Questão de PET - Vemos a Matemática em muitas obras de arte. Uma delas é o calçadão
1 – Vemos a Matemática em muitas obras de arte. Uma delas é o calçadão de Copacabana na cidade do Rio de Janeiro.
Observe a imagem no plano cartesiano abaixo e cumpra as orientações a seguir.
I) Transladar essa imagem horizontalmente para a direita oito unidades, duas vezes seguidas (a primeira em relação à imagem original e, a segunda, em relação à imagem transladada), formando uma figura constituída por três imagens consecutivas e congruentes à original;
II) Transladar a figura resultante da orientação I verticalmente para baixo quatro unidades, formando uma figura constituída por duas figuras congruentes à figura resultante da orientação I.
III) Verifique se a imagem final, resultante das orientações I e II, é semelhante ao calçadão de Copacabana.
RESPOSTA:
Questão de PET - No plano cartesiano abaixo, temos a metade de uma figura
4 – No plano cartesiano abaixo, temos a metade de uma figura, que é simétrica em relação ao eixo y. Determine as coordenadas dos pontos marcados no plano. Em seguida, marque, nesse plano, o simétrico desses pontos em relação ao eixo y e desenhe a outra metade da figura.
RESPOSTA:
Questão de PET - Nas ilustrações abaixo, a linha tracejada indica o eixo de simetria
3 – Nas ilustrações abaixo, a linha tracejada indica o eixo de simetria. Desenhe a figura simétrica em cada uma das ilustrações.
RESPOSTA:
Questão de PET - Anderson desenhou, no plano cartesiano abaixo, metade de uma figura
2 – Anderson desenhou, no plano cartesiano abaixo, metade de uma figura, que é simétrica em relação ao eixo y.
Observe e responda as questões a seguir.
a) Quais são as coordenadas dos seis vértices da figura, os quais se encontram plotados no plano cartesiano?
b) Quais são as coordenadas dos quatro vértices que teremos que determinar para concluir a figura?
c) O que devemos fazer em relação às coordenadas dos quatro vértices plotados no plano e não pertencentes ao eixo y para obter os quatro vértices restantes para completar a figura?
A) Manter a abscissa e manter a ordenada.
B) Manter a abscissa e multiplicar a ordenada por – 1.
C) Multiplicar a abscissa por – 1 e manter a ordenada.
D) Multiplicar a abscissa por – 1 e multiplicar a ordenada por – 1.
d) O que fizemos foi determinar o simétrico, em relação ao eixo y, dos quatro vértices plotados no plano e não pertencentes a esse eixo. Por que não precisamos determinar o simétrico, em relação ao eixo y, dos outros dois vértices plotados no plano e que pertencem a esse eixo?
RESPOSTA:
Questão de PET - Marimar está utilizando o jogo de xadrez para trabalhar
1 – Marimar está utilizando o jogo de xadrez para trabalhar Matemática com seus alunos. Ela apresentou o tabuleiro ao lado e o comparou a um plano cartesiano. Após verificarem em qual quadrante o peão está, ela solicitou que os alunos desenhassem esta peça nos outros três quadrantes do plano cartesiano. Não em qualquer lugar, mas sim o simétrico desta peça em relação à origem do plano cartesiano, em relação ao eixo x e em relação ao eixo y. Desenhe o peão nessas três novas posições.
RESPOSTA:
Questão de PET - Marque, no plano cartesiano abaixo, os vértices A, B, C e D de um retângulo
4 – Marque, no plano cartesiano abaixo, os vértices A, B, C e D de um retângulo, cujas coordenadas são: A (1, 1), B(5, 1), C(1, 4) e D (5, 4). Em seguida, multiplique as coordenadas dos vértices A, B, C e D pelo número inteiro – 2 e marque as novas coordenadas nesse plano cartesiano, formando um novo polígono. Verifique em qual quadrante o segundo polígono se encontra. Compare as medidas do perímetro e da área desses dois polígonos. Anote suas observações.
RESPOSTA:
quarta-feira, 23 de dezembro de 2020
Questão de PET - Considere um conjunto de 10 frutas em que 3 estão estragadas
05 - Considere um conjunto de 10 frutas em que 3 estão estragadas. Escolhendo, aleatoriamente, 2 frutas desse conjunto, determine a probabilidade de:
a) ambas não estarem estragadas.
b) pelo menos uma estar estragada.
RESPOSTA:
Questão de PET - Em uma caixa há 5 papeletas, numeradas de 1 a 5
04 - Em uma caixa há 5 papeletas, numeradas de 1 a 5. Retiram-se duas delas ao acaso e calcula-se a soma dos números escritos nessas duas papeletas. Relacione os elementos que formam os seguintes eventos:
a) a soma ser um número par e múltiplo de 3.
b) a soma ser um número ímpar ou múltiplo de 3.
c) a soma ser um número múltiplo de 7.
RESPOSTA:
Questão de PET - Classifique os eventos a seguir em impossíveis
03 - Classifique os eventos a seguir em impossíveis, certos, muito prováveis (probabilidade maior que 50%) e pouco prováveis (probabilidade menor que 50%).
a) Sair um número 7 no lançamento de um dado comum.
b) Sair um número maior que 2 no lançamento de um dado comum.
c) Sair uma soma maior que 1 no lançamento de dois dados comuns.
d) Sair os números 2, 4, 16, 24, 40, 43 entre os números sorteados na Mega Sena.
RESPOSTA:
Questão de PET - Determine o espaço amostral dos experimentos
02 - Determine o espaço amostral dos experimentos aleatórios a seguir e o número de elementos desse espaço.
a) Retirar uma bola de uma urna contendo 10 bolas numeradas de 1 a 10.
b) Lançar dois dados e observar os resultados possíveis.
RESPOSTA:
Questão de PET - No lançamento de dois dados, um branco e um vermelho
01 - No lançamento de dois dados, um branco e um vermelho, qual é a probabilidade de se obter, nas faces voltadas para cima, a soma do número de pontos maior que 7?
• Vamos encontrar o espaço amostral, preenchendo a tabela abaixo:
• Agora, complete as frases a seguir para responder à pergunta do problema.
O espaço amostral Ω é composto por ____ elementos.
Vamos chamar de A o evento “a soma do número de pontos nas faces voltadas para cima nos dois dados é maior que 7”.
Utilizando a tabela, o número de elementos do evento A é _____.
A probabilidade do evento A é dada por _______.
RESPOSTA:
segunda-feira, 21 de dezembro de 2020
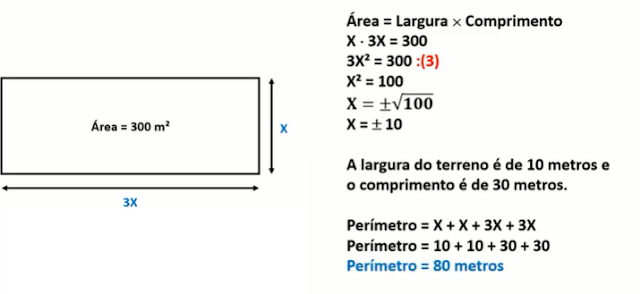
Questão de PET - Um lote retangular possui 300 m² de área
4 – Um lote retangular possui 300 m² de área. Sabe-se que o comprimento desse lote é igual ao triplo de sua largura. Quanto mede o perímetro desse lote?
RESPOSTA:
Assinar:
Comentários (Atom)
LISTAS DE EXERCÍCIOS DE BIOLOGIA / COMPOSIÇÃO QUÍMICA DOS SERES VIVOS
- Exercícios de Biologia sobre aminoácidos - com gabarito
- Exercícios de Biologia sobre a Água - com gabarito
- Exercícios de Biologia sobre a Bioquímica - com gabarito
- Exercícios de Biologia sobre a Vida e Composição Química dos Seres Vivos - com gabarito
- Exercícios de Biologia sobre a Vida e Energia - com gabarito
- Exercícios de Biologia sobre as Enzimas - com gabarito
- Exercícios de Biologia sobre as Proteínas - com gabarito
- Exercícios de Biologia sobre as Vitaminas - com gabarito
- Exercícios de Biologia sobre carboidratos - com gabarito
- Exercícios de Biologia sobre os Lipídios - com gabarito
- Exercícios de Biologia sobre os Sais Minerais II - com gabarito
LISTAS DE EXERCÍCIOS DE BIOLOGIA / CITOLOGIA
- Exercícios de Biologia sobre a Citologia - com gabarito
- Exercícios de Biologia sobre a divisão celular - com gabarito
- - Exercícios de Biologia sobre a Introdução à Citologia e às Membranas Celulares - com gabarito
- Exercícios de Biologia sobre as Mitocôndrias I - com gabarito
- Exercícios de Biologia sobre as Mitocôndrias II- com gabarito
- Exercícios de Biologia sobre as organelas celulares I - com gabarito
- Exercícios de Biologia sobre as organelas celulares II - com gabarito
- Exercícios de Biologia sobre Bioquímica Celular - com gabarito
- Exercícios de Biologia sobre meiose - com gabarito
- Exercícios de Biologia sobre mitose - com gabarito
- Exercícios de Biologia sobre núcleo celular - com gabarito
- Exercícios de Biologia sobre o Complexo de Golgi - com gabarito
- Exercícios de Biologia sobre o Metabolismo Energético da Célula - com gabarito
- Exercícios de Biologia sobre o Núcleo e a Divisão Celular - com gabarito
- Exercícios de Biologia sobre o Retículo Endoplasmático Liso - com gabarito
- Exercícios de Biologia sobre organização celular I - com gabarito
- Exercícios de Biologia sobre organização celular II - com gabarito
- Exercícios de Biologia sobre os Citoplasmas e as Organelas - com gabarito
- Exercícios de Biologia sobre os Lisossomos I - com gabarito
- Exercícios de Biologia sobre os Lisossomos II- com gabarito
- Exercícios de Biologia sobre os Ribossomos - com gabarito
- Exercícios de Biologia sobre respiração celular - com gabarito
- Exercícios de Biologia sobre revestimento celular - com gabarito
- Exercícios de Biologia sobre transportes ativo e passivo - com gabarito